Copper Isotope Alignments
2016 - 4 - 4
[This is a very advanced document. It is recommended one first
become familiar with the NMR Fractals Document , and as well the
technical basics of NMR gyration The Basics of NMR .]
With the discovery of the NMR table values for a zero point magnetic
field, NMR Fractal Chart , a background state of the elements in free space, as powered
from the outer boundary of the universe, it was noticed that we can now
cut a specific length of copper wire and align all the nuclear spin
states in any angular direction we would choose to calculate on the
length of a wire or a tube. With the further discovery of the 33 degree cone
patterns Elementals which will set up three more coupled lengths off the height,
cone side length, cone diameter, and cone circumference, we can
also fix other angles on a length of copper wire for different
spin alignments. Walter Russell Cones . There is now the possibility to formulate a method to
generate power from the nuclear levels of the copper itself and turn
the copper into a battery.
The Challenge
Copper has two independent Isotopes, and either can be
controlled separately yet simultaniously using resonant fractal
lengths. A new goal was realized.
In previous experiment, we verified, both can be aligned into one
angular alignment using the sum of the two Isotope resonant lengths.
Now we will move instead into the operation of vector addition techniques.

Is there a way to set the two isotopes in a geometric divided
alignment, such that the copper itself can become a source of electric
current?
We adjust the two spin angles to operate against one another by
calculating a resultant vector between the two and cut the length of
the copper to that value, fixing the angle of separation between the
two isotopes via a resonance length. There is more then one way to use vector addition,
however consider we want the two spin angles to cross at one consistant
angle, through all the atoms inside the copper element.
Angle of Separation
A few different angles of alignment were considered here to set the two
Isotopes at angle with respect to one another, and tables were
calculated using geometry to accomplish this task.
The spreadsheet below, was set up with 90 degree and 33 degree separations, for testing with SS Calipers on a copper tube.
The upper calculation table used the abundance value times the Isotope length as the height of the 33 degree cones.
The lower table uses only the raw Isotope value. Ratios are compared
between all the different cone segment lengths for each Isotope, as the
angle of spin can be manipulated using any one of the segmented values.
In 90 degree manipulation we calculate the sum of the squares, then take the square root.
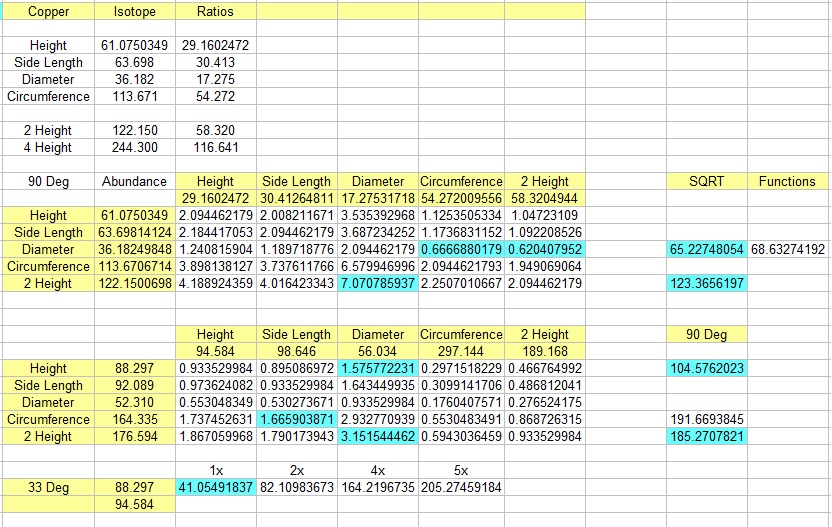
NMR Spreadsheet [OpenOffice.Org]
Of notable energy, using a SS caliper, the 33 degree alignment seems to offer the closest feeling to an electric field.
Across the bottom are the segmented values starting with 41.0549 mm moving to the right with longer multiple lengths.
This geometric calculation is shown below.
33 Degree Separation Angle Vector Geometry
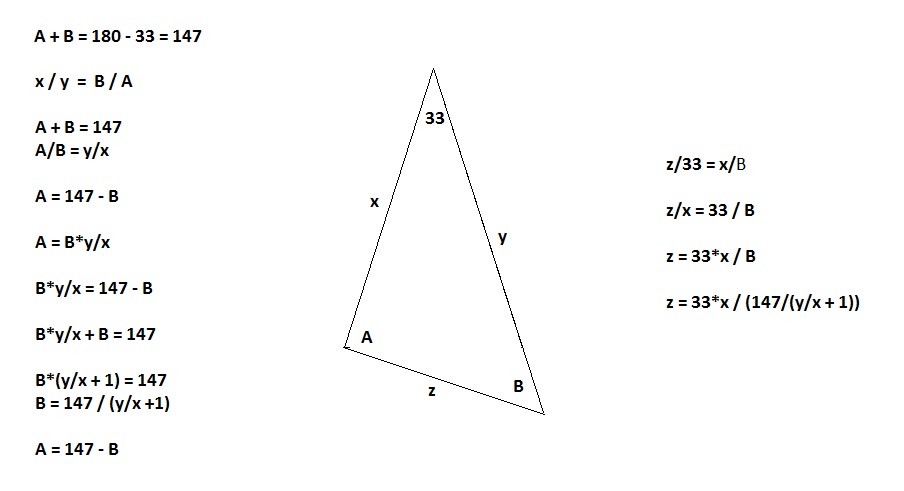
Note that a sum of all the angles in a triangle must add up to 180
degrees. The two Isotope frequencies are represented by X and Y, and
the differential frequency will be Z the unknown manipulator alignment.
Using two equations combined simultaneously, we determine the resultant
length Z for any angle we might choose to set up between the Isotopes,.
In the diagram above 33 degrees was the choice.
You can substitute any angle you would desire where you see 33,
and this will alter the 147 as well, as all the angles must add up to
180 degrees.
Y = the longer NMR value = 94.584 (Cu65) Abundance 30.83
X = the shorter NMR value = 88.297 (Cu63) Abundance 69.17
Z = the angular adjustment value to hold the two in a fixed relationship at 33 degrees of separation
Z = 41.0549 mm [See spreadsheet above, bottom line]
A piece of copper accurately cut to a length of 41.0549 mm or cm will
set up this angular skew between the two Isotopes in the copper atoms,
and create a spin against spin torque inside the copper.
Some vibration will be output from the copper, originating on the nuclear levels.
Since we are using NMR vectors, it may be an electrical or magnetic charged result.
Remember, these NMR length do not need any external field applied to
them or the angle will be dislodged to align with it instead.
The Z vector will be running the length of the copper element, and both x and y
will align to one side of the length and spin against one another on
the diameter and circumference values of each.
Note also the Y atoms, will appear every 30.83 percent of all the
atoms, and the X atoms will be 69.17 percent of all the atoms in any
length of copper cut on planet earth.
This is found in the NMR table and listed as Abundance in percent value.
The two spin forces will not be equal, due to abundance issue. This
may be a good thing, and hopefully it will create a low frequency
oscillation as the two beat against one another.
Vector Addition Method 2
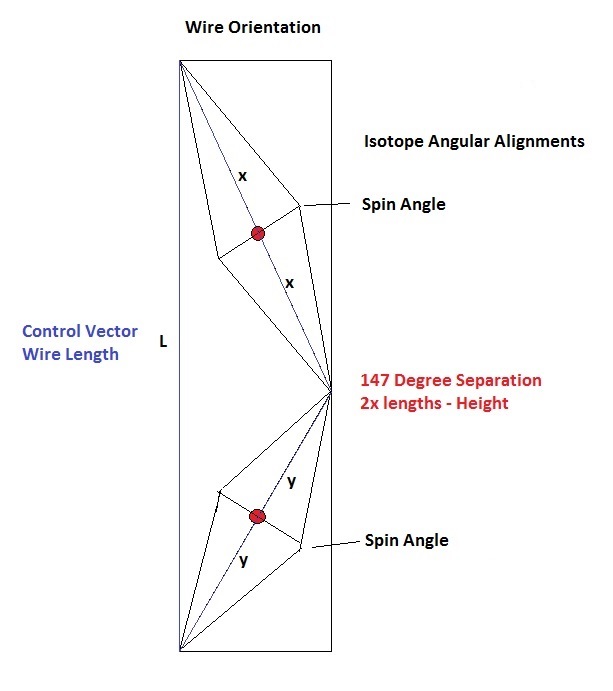
[Copper Wire Alignment 2x]
If you lock in the electric field, the torsion field will spin around
it. If you lock in the torsion field, the electric field will spin
around it. AC electricity is a rotation between both alignments in the
wire at some frequency.
Height of the single cone represents the electric field, and
diameter of the cone represents the torque or torsion spining
around it. 16.5 degree side length represents a compressing or expanding magnetic field spining along the electric vector.
In this technique we consider the whole atom or a 2x version of the
cones. Red dots are center of nuclear mass points. In the diagram we only show
the inverted cone set, but the application is clear. Each isotope will
fold back on the other at an angle of 147 degrees, so that the two spin
angles intersect at 33 degrees. Diagram is not to scale, for mental
reference only. In this way the geometric pattern will move up the wire
as each isotope creates a different spin angle across it's width. The
sum of both angles should be equal to 33 degrees. Our control vector now
comes out longer then the two, but also shorter then the linear sum of
both, setting the two spins up to create a torsion against one another,
each fighting for control of the coherent nuclear field in the coppers
mass.
There will be two calculations, as in the one we will compensate to
balance the Abundance ratio, and in the second we will only calculate
the raw NMR fractals as singular atoms, as we did each before in the first
spread sheet.
Height Times Abundance
If we set 10,000 atoms of copper in a line, 3083 of them will
vibrate at 94.584 mm, and 6917 of them will vibrate at 88.297 mm T
field wavelength fractal.
For full atoms we use a 2x version of the height to move across the
atoms dual cone field, offering expansion and contraction from the
nuclear center outwards in two directions. As with the 33.3 to 66.6, a
2x is necessary to expose and separate all three points in space.
X = 94.584 * 2 * 3083 = 583,204.944
Y = 88.297 * 2 * 6917 = 1,221,500.698
We are now left with a similar geometric calculation of vector sums, as
we used last time to solve for the Z vector value, to cut a wire length
that will hold this pattern at the nuclear level.
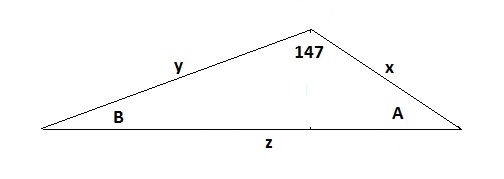
X / Y = B / A
A + B = 33
A = 33 - B
A/B = Y/X
A = B*Y/X
B*Y/X = 33 - B
(B*Y/X)+B = 33
B*(Y/X+1) = 33
B = 33 / (Y/X + 1) = 10.664 Deg
A = 33 - B = 22.336 Deg
Z / 147 = X / B
Z / X = 147 / B
Z = 147*X / B
Z = 147 * X / ( 33 / (Y/X +1)) = 8,039,143.314
Z = 147 * X / (33 / 3.094)
Z = 147 * X / 10.6658047
[Watch for further experimental trials.]




